⬇️ My Thoughts ⬇️
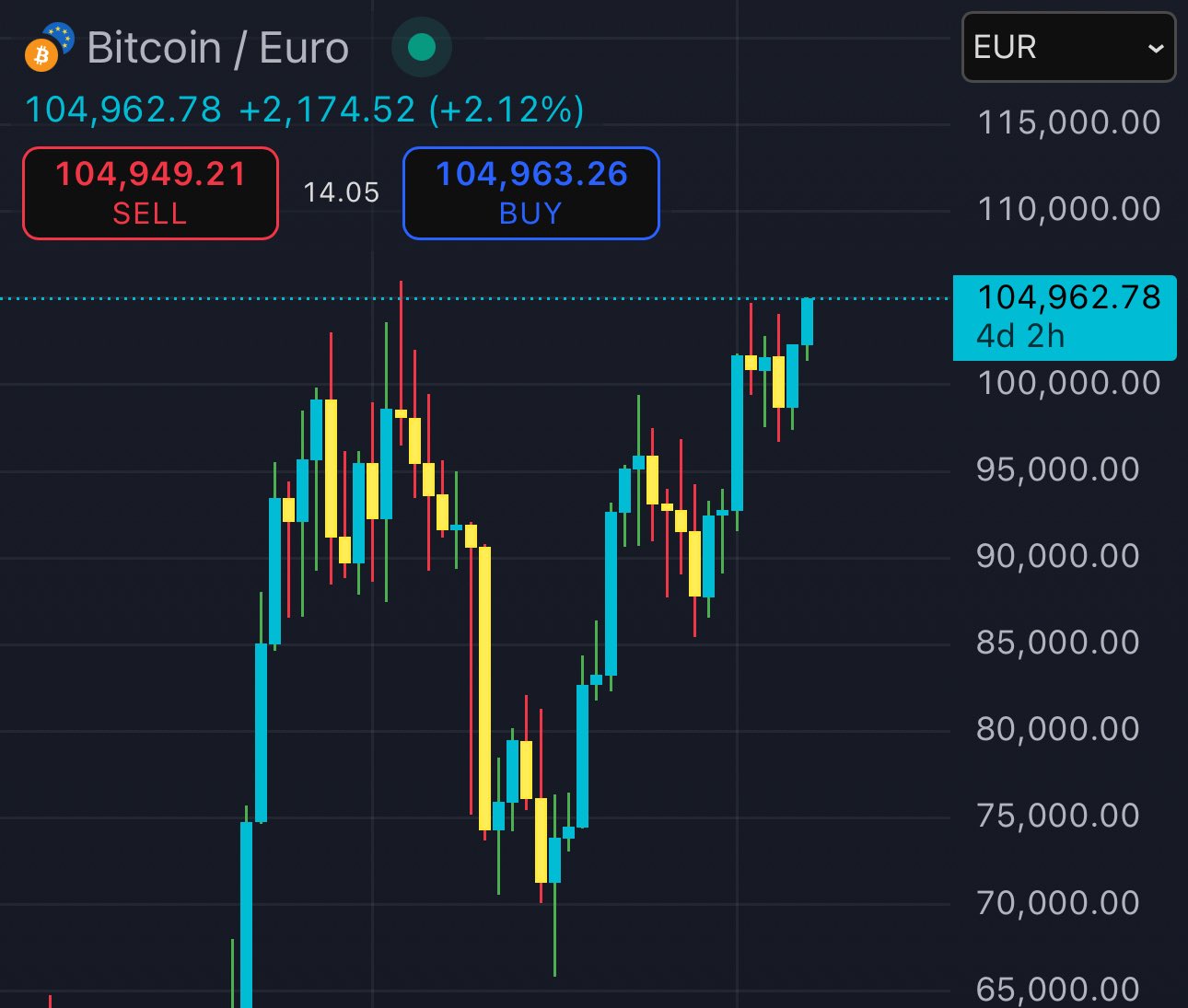
and soon the Eurozone will join the new BTC all time high party 🇪🇺🥳 Bitcoin still hasn't seen a new high in EUR since January 2025 this happened to due the relative appreciation apprtetiation of Euro against US dollar
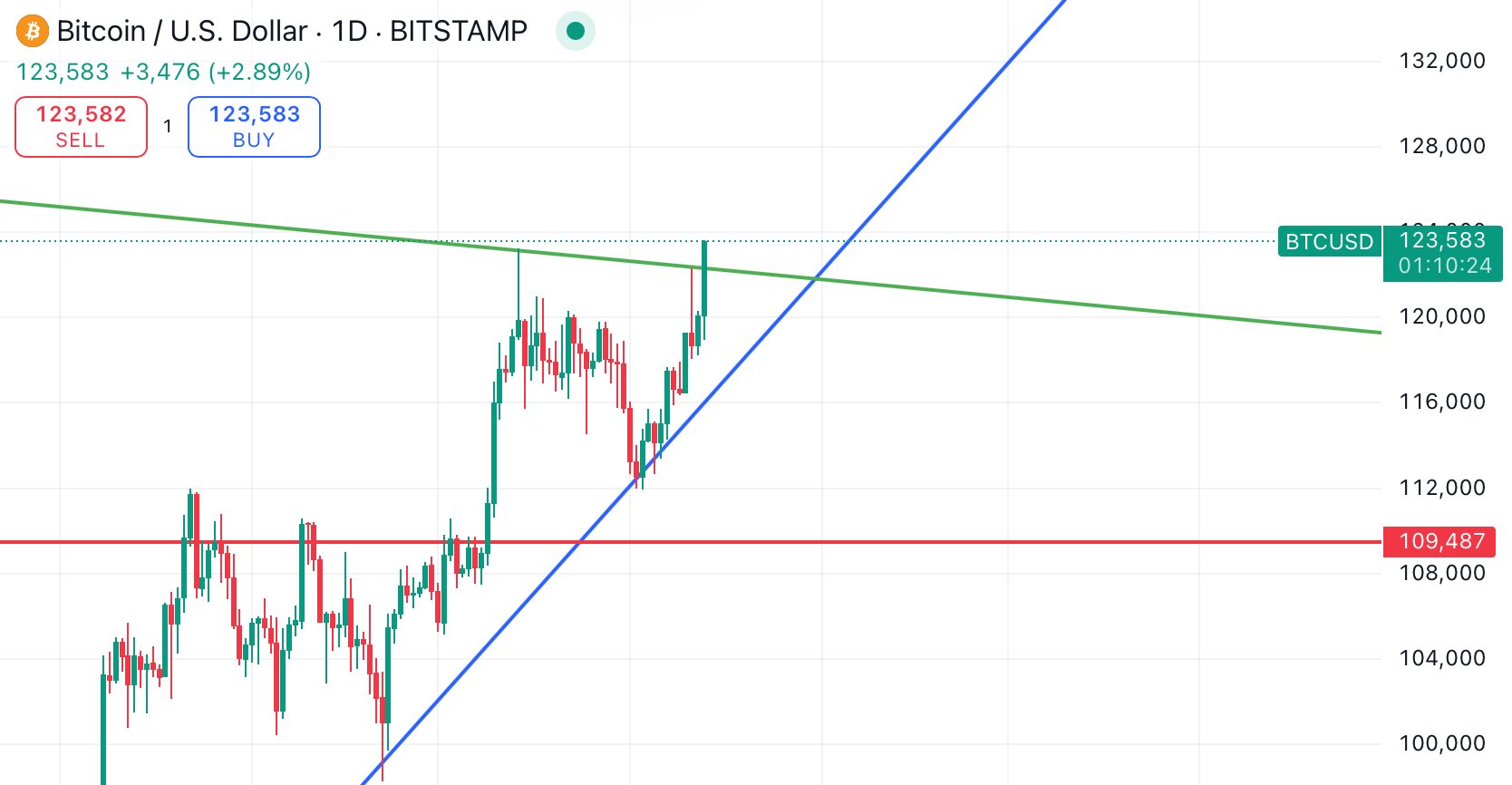
and there you go, Bitcoin reached a new all time high 😄 notice how precisely it respect the trend lines
and there you go, Bitcoin reached a new all time high 😄 notice how precisely it respect the trend lines
bitcoin went up 6% from the weekly support line until the end of this month, bitcoin will either see a new all time high or retest the ≈$0.1095M support this is the daily timescale of the same chart - the blue and red lines are weekly, green is daily just a quick check-up
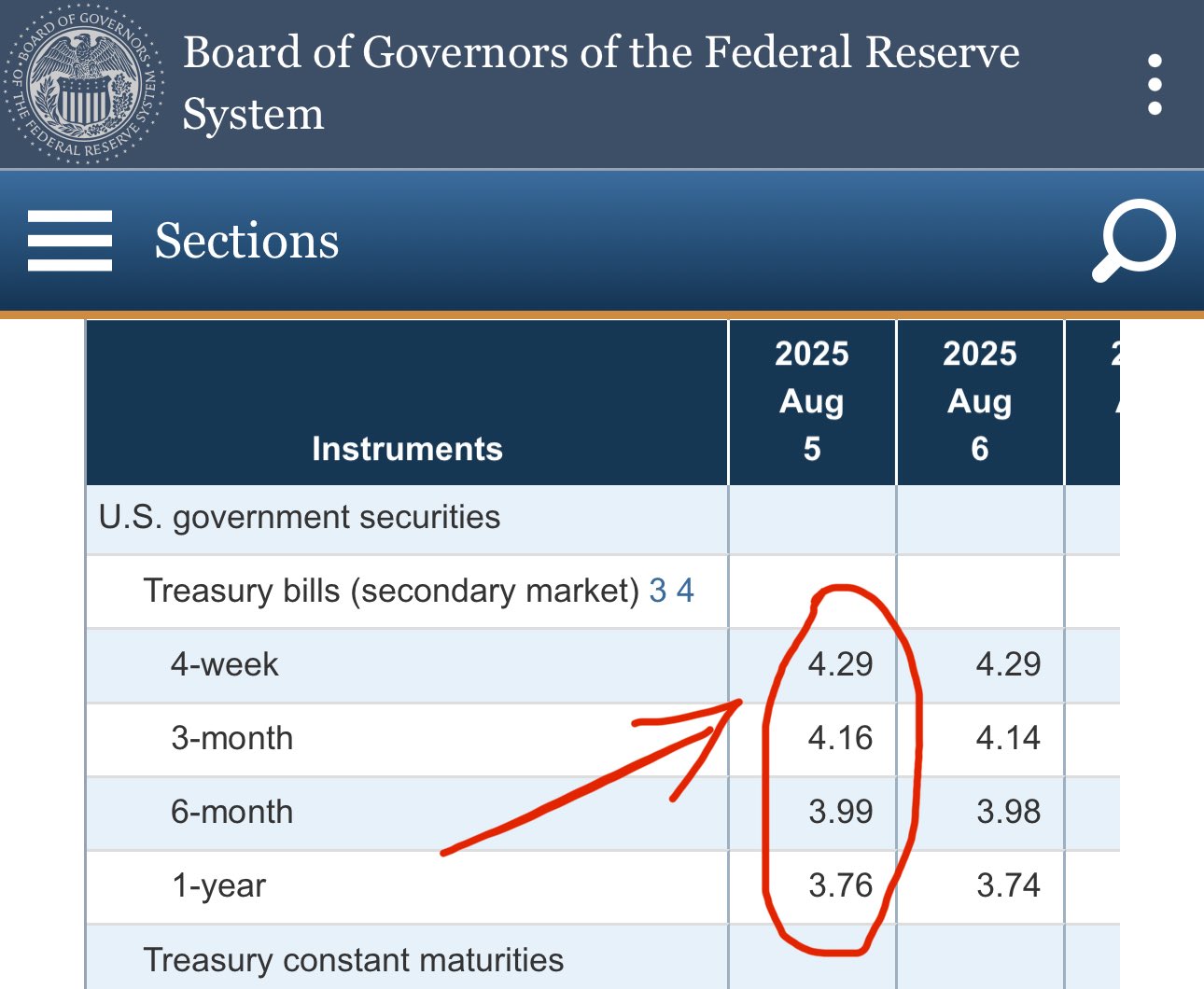
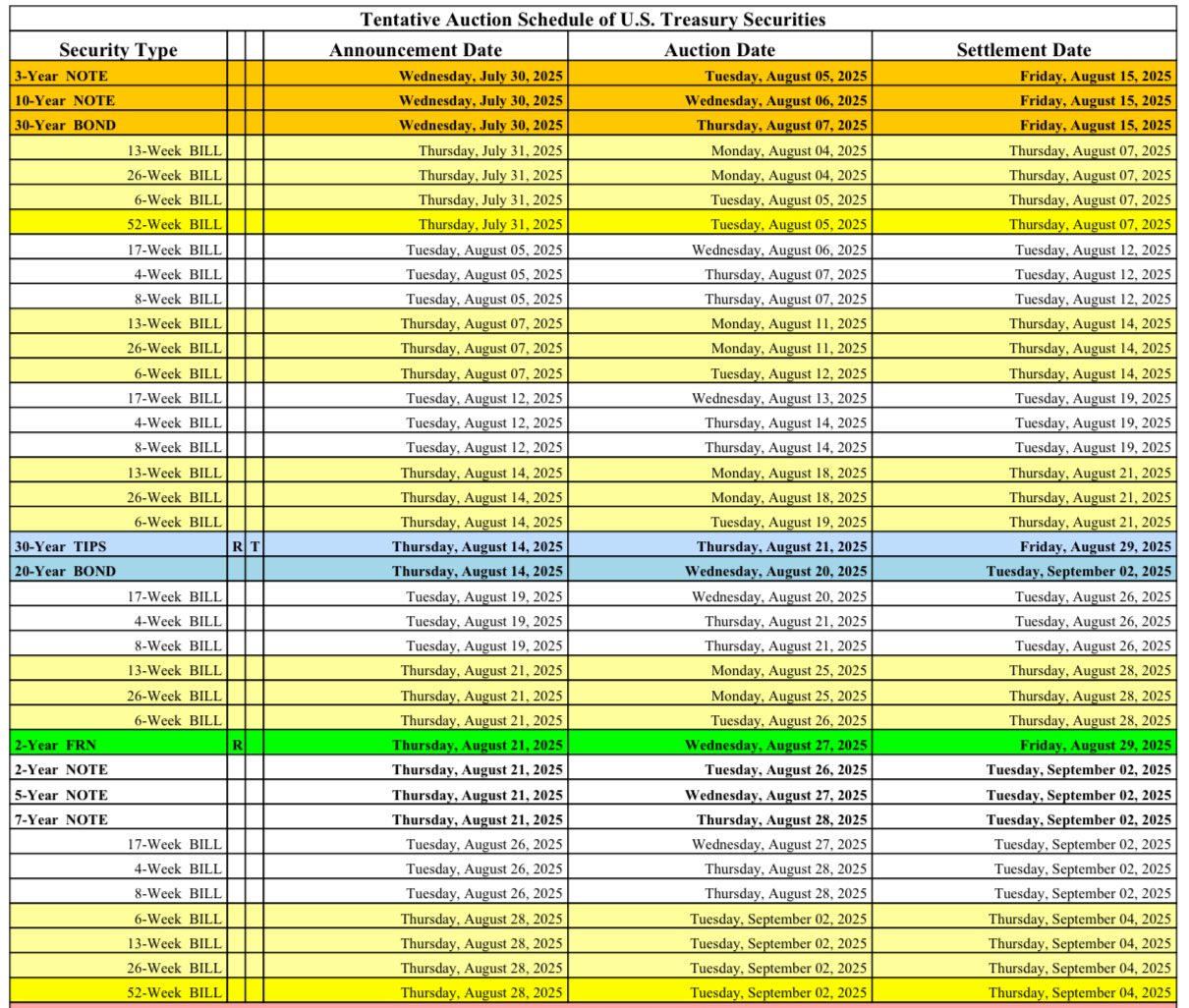
so according to this, since Treasuries yield more than ON RRP the wholesale cash moved from ON RRP into Treasuries when the US Treasury spends them - they flow right back into broad money indeed, currently T bills yield from 4.29%, while ON RRP is at 4.25% interesting take!
the US treasury is doing exactly that - issuing short-term debt to retire/repurchased long-term debt that's effectively refinancing longer-term debt with shorter-term debt. this shorter-term debt will also need to be refinanced, but now much sooner
this is why duration matching is key for financial institutions this is also the reason why it's generally not a good idea for governments to refinance long-term debt with short-term debt this shortens the duration of both - government liabilities and market's assets
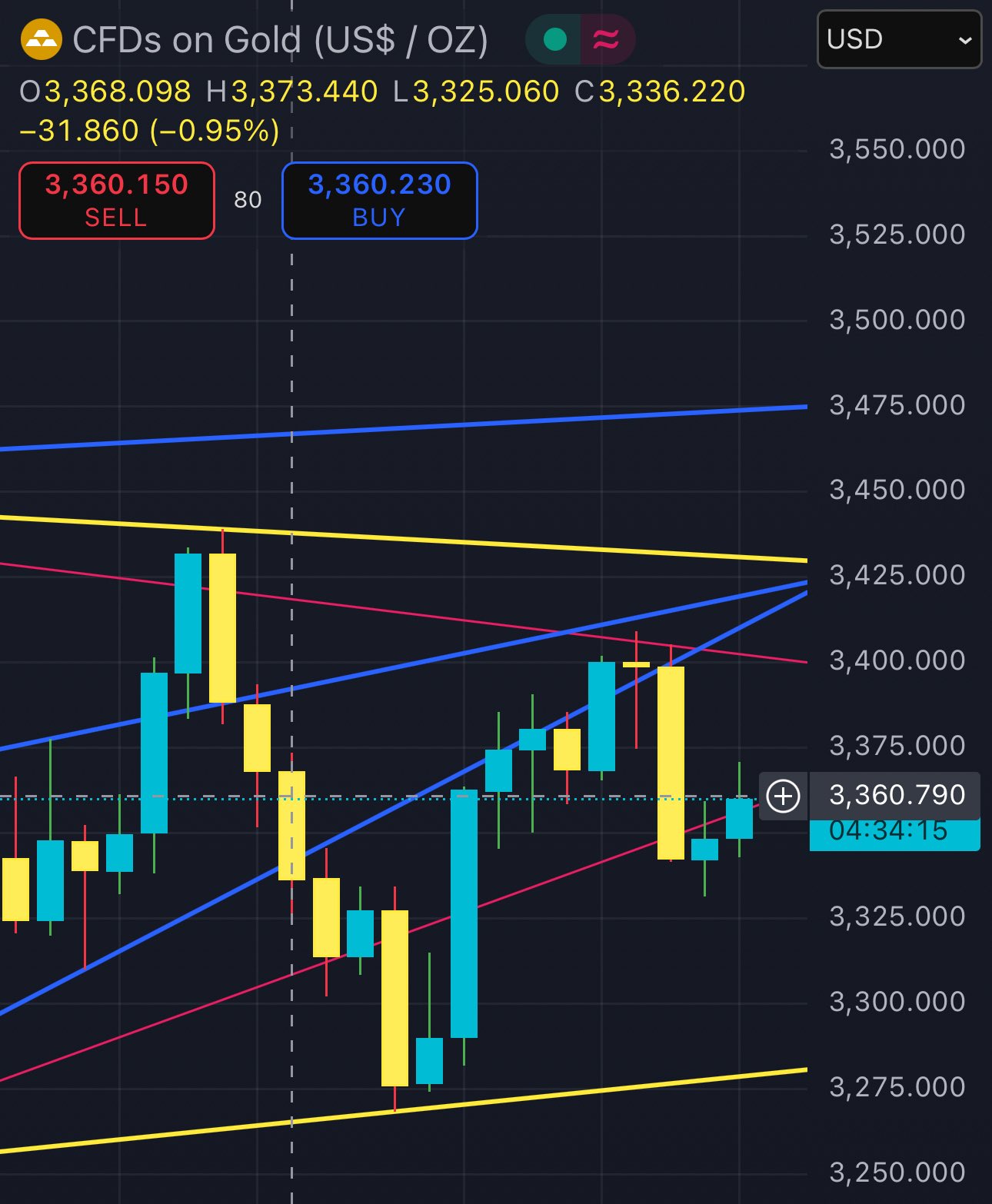
gold is in the same price range as when the US dollar index was ≈97.7 on July 25th 2025 if DXY hits ≈97.1 - expect gold to retest ≈$3440. this time with a stronger support build up by price action this could definitely be what pushes gold to a new all time high
re-iterating on the 1.5 month old thread 😄 inflation is still here to stay and gold is still yet to do something - but it sure will
this is why duration matching is key for financial institutions this is also the reason why it's generally not a good idea for governments to refinance long-term debt with short-term debt this shortens the duration of both - government liabilities and market's assets
duration matching protects: ➖ liquidity via cashflow modulation, by helping liability cashflows match asset cashflows ➖ solvency via asset and liability value modulation, by reducing asset value loss when yields fall and reducing liability value loss when yields raise
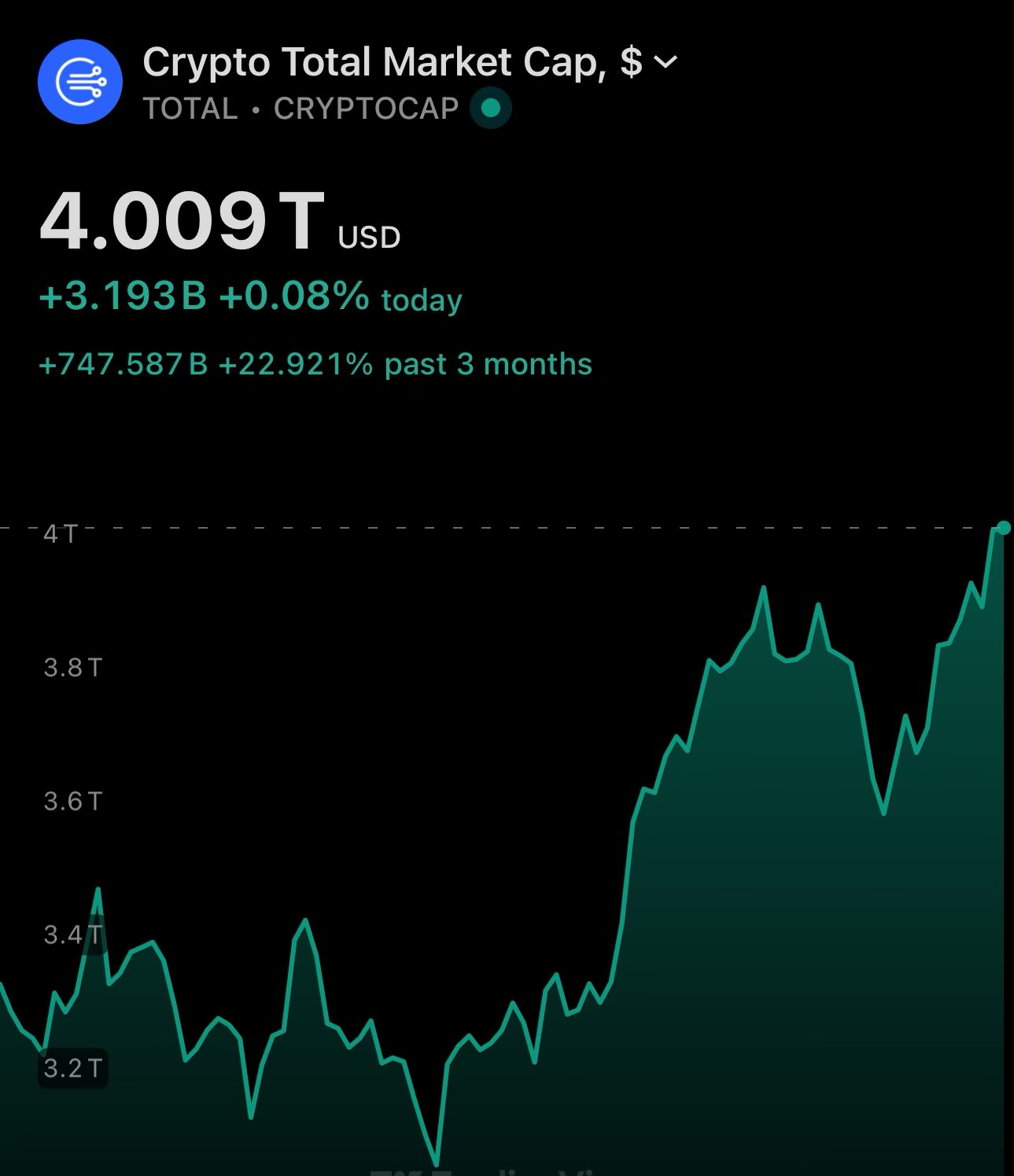
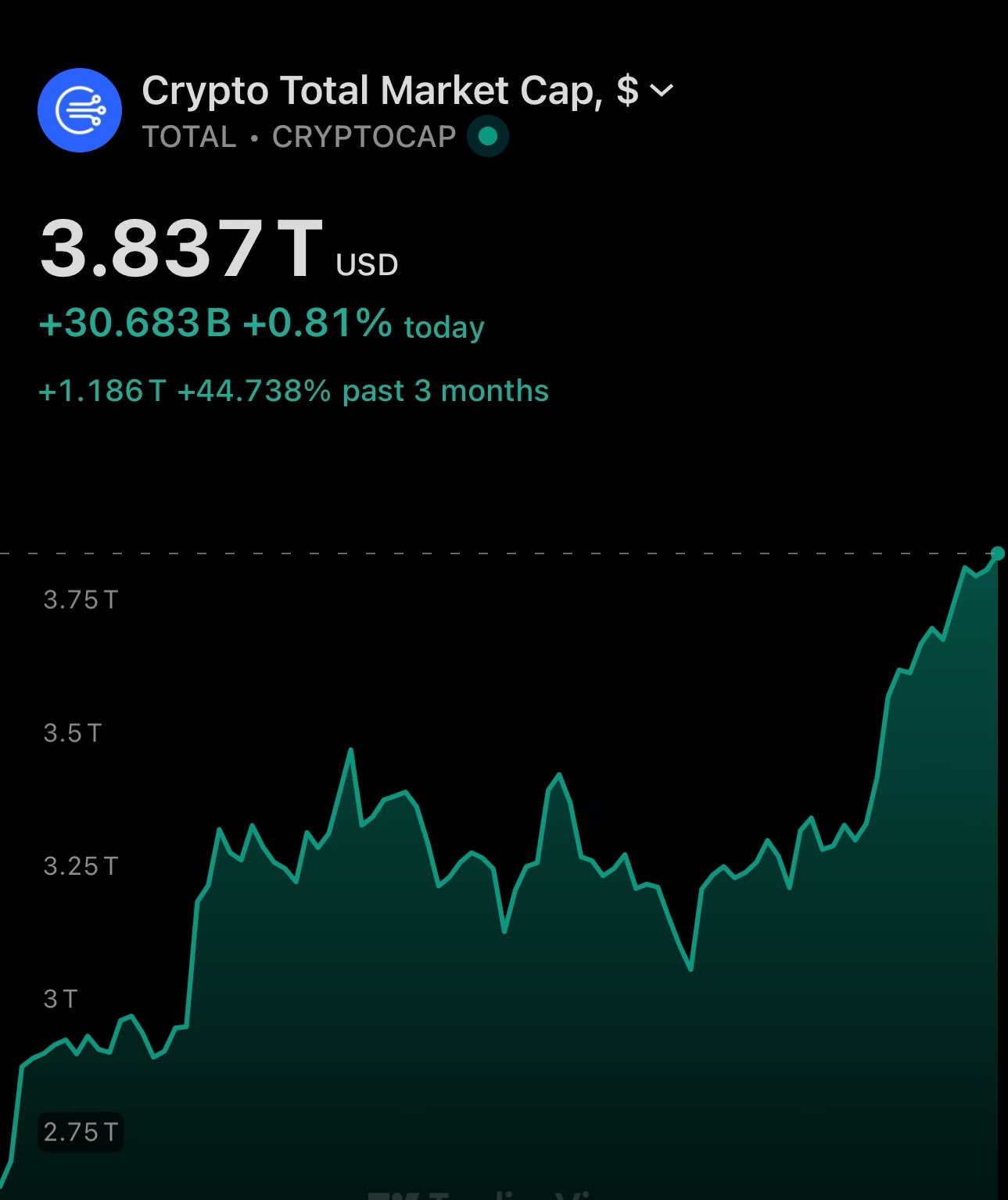
and the crypto market cap has now been sitting at $4 trillion for the 3rd day 🤝
🚀 and indeed the crypto cap increased even more now, await for a solid $4 Trillion it's almost like it's correlated with global liquidity flows - or perhaps I'm just really good at guessing 😳 i wrote a lot about this in the past - so read up for details if inerested!
duration matching protects: ➖ liquidity via cashflow modulation, by helping liability cashflows match asset cashflows ➖ solvency via asset and liability value modulation, by reducing asset value loss when yields fall and reducing liability value loss when yields raise
duration matching protects liquidity and solvency by modulating yield shift effects on the value of assets and liabilities
duration matching protects liquidity and solvency by modulating yield shift effects on the value of assets and liabilities
since a 30 year bond discounts 30 years of cashflows and those cashflows directly incorporate this compounding yield - its price moves more with yields than a comparable, shorter time to maturity bond
since a 30 year bond discounts 30 years of cashflows and those cashflows directly incorporate this compounding yield - its price moves more with yields than a comparable, shorter time to maturity bond
regarding 1 year vs 30 year bond - imagine yields rise by 2%: ➖ the price of the bond maturing in 1 year declines by discounting those 2% from 1 year of cashflows ➖ a 30 year bond discounts for 30 years of cashflows
regarding 1 year vs 30 year bond - imagine yields rise by 2%: ➖ the price of the bond maturing in 1 year declines by discounting those 2% from 1 year of cashflows ➖ a 30 year bond discounts for 30 years of cashflows
the longer the bond's time to maturity - the more compounding of unfavorable yields the bond's price must incorporate the more technical term is discounting, but compounding of unfavorable yields may help in bulging the mental model for what happens
the longer the bond's time to maturity - the more compounding of unfavorable yields the bond's price must incorporate the more technical term is discounting, but compounding of unfavorable yields may help in bulging the mental model for what happens
larger modified duration value means that the bond's price is more sensitive to changes in bond yields this makes sense. the longer the time to maturity - the longer the risk and term premia comes into play
larger modified duration value means that the bond's price is more sensitive to changes in bond yields this makes sense. the longer the time to maturity - the longer the risk and term premia comes into play
modified duration quantifies how much a bond’s price will change for a 1% change in bond yields while the bond pays fix sums - its market value/price varies, so its yield is not fixed
modified duration quantifies how much a bond’s price will change for a 1% change in bond yields while the bond pays fix sums - its market value/price varies, so its yield is not fixed
that's a problem because the market price of the bond may have fallen significantly and the rest of the bond payment - 1.5% coupon + principal needs to be re-financed at potentially unfavorable rates
that's a problem because the market price of the bond may have fallen significantly and the rest of the bond payment - 1.5% coupon + principal needs to be re-financed at potentially unfavorable rates
the bank's only option now is to sell the UST bond they hold at the market price, and use the proceeds to settle the 1.5% semiannual coupon liability
the bank's only option now is to sell the UST bond they hold at the market price, and use the proceeds to settle the 1.5% semiannual coupon liability
now the bank has an issue - the 1.5% liability payment is in 6 months, while 4% yield from the asset financed by that liability only gets paid in 1 year while the bank will have the money to pay in the future - it doesn't have it now
now the bank has an issue - the 1.5% liability payment is in 6 months, while 4% yield from the asset financed by that liability only gets paid in 1 year while the bank will have the money to pay in the future - it doesn't have it now
what would happen if the bank issued bonds with a semi-annual coupon instead? semi-anual coupon means that bondholders get 2 ≈1.5% interest payments in the year: at 6 months, and maturity remember: the UST bond only has one payment - at maturity in 1 year (think zero-coupon)
what would happen if the bank issued bonds with a semi-annual coupon instead? semi-anual coupon means that bondholders get 2 ≈1.5% interest payments in the year: at 6 months, and maturity remember: the UST bond only has one payment - at maturity in 1 year (think zero-coupon)
assume that both start simultaneously and mature in 1 year without any periodic payments this means that today the bank borrows $100M at 3% APY and invests it at 4% in exactly 1 year the bank receives $104M from the UST bond, repays $103M to bondholders and keeps $1M profit
assume that both start simultaneously and mature in 1 year without any periodic payments this means that today the bank borrows $100M at 3% APY and invests it at 4% in exactly 1 year the bank receives $104M from the UST bond, repays $103M to bondholders and keeps $1M profit
let's say the bank issued bonds (liability) at 3% and acquired UST bonds (asset) with a 4% yield both assets and liabilities have a transaction amount of $100 million the bank uses the loan (issued bond) to purchase higher yield UST bonds, thus profiting a ≈1% spread
let's say the bank issued bonds (liability) at 3% and acquired UST bonds (asset) with a 4% yield both assets and liabilities have a transaction amount of $100 million the bank uses the loan (issued bond) to purchase higher yield UST bonds, thus profiting a ≈1% spread
let's develop on this simple bank example assume a brand-new bank with an empty balance sheet, no revenue, no deposits, no cashflow and no regulations the bank is about to finance its first asset - a UST bond with a liability - bonds issued by the bank
let's develop on this simple bank example assume a brand-new bank with an empty balance sheet, no revenue, no deposits, no cashflow and no regulations the bank is about to finance its first asset - a UST bond with a liability - bonds issued by the bank
this newly acquired UST bond was financed with some liability of the bank let's say the bank itself issued bonds with a smaller coupon than UST’s thus, the bank used a liability to finance and asset and earns a spread
this newly acquired UST bond was financed with some liability of the bank let's say the bank itself issued bonds with a smaller coupon than UST’s thus, the bank used a liability to finance and asset and earns a spread
a bank may buy a US Treasury bond (UST) and hold it as an asset. at some point, that bond matures, thus terminating its existence
a bank may buy a US Treasury bond (UST) and hold it as an asset. at some point, that bond matures, thus terminating its existence
most of financial institution's assets have an expiration date these assets are mostly composed of loans, debt securities and money market instruments still, all come with an expiration date
most of financial institution's assets have an expiration date these assets are mostly composed of loans, debt securities and money market instruments still, all come with an expiration date
when liabilities become due you must ensure that assets can cover them this means ensuring that cashflow and asset monetization provides enough liquidity to settle the debt, plus a desired spread
when liabilities become due you must ensure that assets can cover them this means ensuring that cashflow and asset monetization provides enough liquidity to settle the debt, plus a desired spread
duration matching protects solvency and liquidity when yields shift assets are financed by liabilities and equity. financial institutions like banks usually have small equity - so liabilities finance assets
